Bilo je obdobje, ko je bilo treba med telefonskim klicem na oddaljene kraje postaviti usta zelo blizu oddajnika, govoriti zelo počasi in zelo glasno, tako da lahko oseba na drugem koncu jasno sliši sporočilo. Danes lahko celo vodimo video klice po vsem svetu z visokokakovostnimi ločljivostmi. Skrivnost tako izjemnega razvoja tehnologije je v tem Električna filter teorija in Teorija daljnovoda . Električni filtri so vezja, ki prepuščajo le izbrani frekvenčni pas, medtem ko druge neželene frekvence dušijo. Eden takih filtrov je Visokoprepustni filter .
Kaj je visokofrekvenčni filter?
Opredelitev visokofrekvenčnega filtra je filter, ki prepušča samo tiste signale, katerih frekvence so višje od mejnih frekvenc, s čimer oslabi signale nižjih frekvenc. Vrednost mejne frekvence je odvisna od zasnove filtra.
Vezje visokofrekvenčnega filtra
Osnovni visokofrekvenčni filter je zgrajen s serijsko povezavo kondenzator in upor . Medtem ko se vhodni signal nanaša na kondenzator , izhod se potegne čez upor .

Vezje visokofrekvenčnega filtra
V tej ureditvi tokokroga ima kondenzator visoko odpornost pri nižjih frekvencah, zato deluje kot odprt tokokrog na nizkofrekvenčne vhodne signale, dokler ni dosežena mejna frekvenca 'fc'. Filter oslabi vse signale pod mejno frekvenco. Pri frekvencah nad odrezano frekvenco reaktanca kondenzatorja postane nizka in deluje kot kratek stik na te frekvence, kar jim omogoča, da preidejo neposredno na izhod.
Pasivni RC visokofrekvenčni filter
Zgornji prikazani visokofrekvenčni filter je znan tudi kot Pasivni visokofrekvenčni RC filter saj je vezje zgrajeno samo z uporabo pasivni elementi . Za delovanje filtra ni treba uporabljati zunanje moči. Tu je kondenzator reaktivni element in izhod se potegne čez upor.
Značilnosti visokofrekvenčnega filtra
Ko govorimo o mejna frekvenca sklicujemo se na točko v frekvenčni odziv filtra kjer je ojačanje enako 50% največjega ojačanja signala, tj. 3dB največjega dobička. Pri visokofrekvenčnem filtru se dobiček poveča s povečanjem frekvenc.

Krivulja frekvence visokofrekvenčnega filtra
Ta mejna frekvenca fc je odvisna od vrednosti R in C vezja. Tu je časovna konstanta τ = RC, mejna frekvenca je obratno sorazmerna s časovno konstanto.
Odsečna frekvenca = 1 / 2πRC
Dobiček v vezju daje AV = Vout / Vin
tj. AV = (Vout) / (V in) = R / √ (Rdva+ Xcdva) = R / Z
Pri nizki frekvenci f: Xc → ∞, Vout = 0
Pri visokofrekvenčnem f: Xc → 0, Vout = Vin
Frekvenčni odziv visokofrekvenčnega filtra ali graf visokofrekvenčnega filtra
V visokofrekvenčnem filtru so vse frekvence, ki ležijo pod mejno frekvenco 'fc', oslabljene. Na tej odrezani frekvenčni točki dobimo -3dB ojačanja in na tej točki bodo reaktanci kondenzatorja in vrednosti upora enaki, tj. R = Xc. Dobiček se izračuna kot
Dobiček (dB) = 20 log (Vout / Vin)
Naklon krivulje visokofrekvenčnega filtra je +20 d B / desetletje, tj. po prehodu nivoja izklopne frekvence se izhodni odziv vezja poveča od 0 do Vin s hitrostjo +20 dB na desetletje, kar je 6 dB povečanje na oktavo.

Frekvenčni odziv visokofrekvenčnega filtra
Območje od začetne točke do presečne frekvenčne točke je znano kot zaustavitveno območje, saj nobena frekvenca ne sme prehajati. Območje od zgornje mejne točke frekvence. točka -3 dB je znana kot pasovni pas . Pri izklopni frekvenci bo amplituda točkovne izhodne napetosti 70,7% vhodne napetosti.
Tukaj pasovna širina filtra označuje vrednost frekvence, s katere smejo signali prehajati. Na primer, če je pasovna širina visokofrekvenčnega filtra podana kot 50 kHz, to pomeni, da lahko prehajajo samo frekvence od 50 kHz do neskončnosti.
Fazni kot izhodnega signala je +450 pri mejni frekvenci. Formula za izračun faznega premika visokofrekvenčnega filtra je
∅ = arktan (1 / 2πfRC)

Krivulja faznega premika
V praksi se izhodni odziv filtra ne razširi v neskončnost. Električna značilnost filtrirnih elementov uporablja omejitev odziva filtra. S pravilnim izborom komponent filtra lahko prilagodimo obseg frekvenc, ki jih bomo oslabili, obseg, ki ga bomo prenesli itd.
Visokofrekvenčni filter z optičnim ojačevalnikom
V tem visokofrekvenčnem filtru dodamo še pasivne filtrirne elemente Op-amp na vezje. Namesto da bi dobili neskončni izhodni odziv, je tu izhodni odziv omejen z odprto zanko značilnosti op-amp . Zato ta filter deluje kot a pasovni filter z ločeno frekvenco, ki je določena s pasovno širino in ojačevalnimi lastnostmi Op-amp.

Visokofrekvenčni filter z optičnim ojačevalnikom
Povečanje napetosti v odprti zanki Op-amp deluje kot omejitev pasovne širine ojačevalnik . Povečanje ojačevalnika se s povečanjem vhodne frekvence zmanjša na 0 dB. Odziv vezja je podoben pasivnemu visokofrekvenčnemu filtru, vendar tu ojačanje Op-amp ojača amplitudo izhodnega signala.
The dobiček filtra uporaba neinvertirajočega Op-amp je podana z:
AV = Vout / Vin = (Izklopljeno (f / fc)) / √ (1+ (f / fc) ^ 2)
kjer je Af ojačanje pasovnega pasu filtra = 1+ (R2) / R1
f je frekvenca vhodnega signala v Hz
fc je mejna frekvenca
Ko nizka toleranca upori in kondenzatorji se uporabljajo ti visoko pasovni aktivni filtri zagotavljajo dobro natančnost in zmogljivost.
Aktivni visokofrekvenčni filter
Visokofrekvenčni filter z optičnim ojačevalnikom je znan tudi kot aktivni visokofrekvenčni filter ker je skupaj s pasivnimi elementi kondenzator in upor aktivni element V vezju se uporablja op-amp . S tem aktivnim elementom lahko nadzorujemo mejno frekvenco in obseg izhodnega odziva filtra.
Visokofrekvenčni filter drugega reda
Filtrska vezja, ki smo jih videli do zdaj, se štejejo za visokofrekvenčne filtre prvega reda. V visokokakovostnem filtru drugega reda se doda dodaten blok RC omrežja visokofrekvenčni filter prvega reda na vhodni poti.
Visokofrekvenčni filter drugega reda
The frekvenčni odziv visokofrekvenčnega filtra drugega reda je podoben visokofrekvenčnemu filtru prvega reda. Toda pri visokokakovostnem visokofrekvenčnem filtru drugega reda bo dvakrat večji kot pri filtru prvega reda pri 40dB / desetletju. Filtre višjega reda lahko oblikujemo s kaskadnimi filtri prvega in drugega reda. Čeprav vrstni red ni omejen, se velikost filtra povečuje skupaj z vrstnim redom in natančnost se poslabša. Če je v filtru višjega reda R1 = R2 = R3 itd ... in C1 = C2 = C3 = itd ..., bo frekvenca odrezanja enaka ne glede na vrstni red filtra.

Visokofrekvenčni filter drugega reda
Mejna frekvenca visokofrekvenčnega aktivnega filtra drugega reda je lahko podana kot
fc = 1 / (2π√ (R3 R4 C1 C2))
Funkcija prenosa visokofrekvenčnega filtra
Ker se impedanca kondenzatorja pogosto spreminja, imajo elektronski filtri frekvenčno odvisen odziv.
Kompleksna impedanca kondenzatorja je podana kot Zc = 1 / sC
Kjer je s = σ + jω, ω kotna frekvenca v radianih na sekundo
Prenosno funkcijo vezja lahko najdemo s standardnimi tehnikami analize vezja, kot je Ohmov zakon , Kirchhoffovi zakoni , Superpozicija itd. Osnovna oblika prenosne funkcije je podana z enačbo
H (s) = (am s ^ m + a (m-1) s ^ (m-1) + ⋯ + a0) / (bn s ^ n + b (n-1) s ^ (n-1) + ⋯ + b0)
The vrstni red filtra je znan po stopnji imenovalca. Poljaki in ničle vezja se pridobijo z reševanjem korenin enačbe. Funkcija ima lahko resnične ali kompleksne korenine. Način, kako so te korenine narisane na ravnini s, kjer je σ označena z vodoravno osjo, ω pa označena z navpično osjo, razkriva veliko informacij o vezju. Za visokofrekvenčni filter je ničla v izvoru.
H (jω) = Vout / Vin = (-Z2 (jω)) / (Z1 (jω))
= - R2 / (R1 + 1 / jωC)
= -R2 / R1 (1 / (1+ 1 / (jωR1 C))
Tukaj H (∞) = R2 / R1, dobiček pri ω → ∞
τ = R1 C in ωc = 1 / (τ), tj. ωc = 1 / (R1C) je mejna frekvenca
Tako je prenosna funkcija visokofrekvenčnega filtra podana z H (jω) = - H (∞) (1 / (1+ 1 / jωτ))
= - H (∞) (1 / (1- (jωc) / ω))
Če je vhodna frekvenca nizka, je Z1 (jω) velika, zato je izhodni odziv nizek.
H (jω) = (- H (∞)) / √ (1+ (ωc / ω) ^ 2) = 0, ko je ω = 0 H (∞) / √2, ko je ω = ω_c
in H (∞), kadar je ω = ∞. Tu negativni znak označuje fazni premik.
Ko je R1 = R2, je s = jω in H (0) = 1
Torej, prenosna funkcija visokofrekvenčnega filtra H (jω) = jω / (jω + ω_c)
Maslo vredno visokofrekvenčnega filtra
Poleg zavračanja neželenih frekvenc mora imeti idealen filter tudi enakomerno občutljivost za želene frekvence. Tako idealen filter je nepraktičen. Toda Stephen Butter v svojem prispevku »O teoriji filtrirnih ojačevalnikov« je pokazal, da je to vrsto filtra mogoče doseči s povečanjem števila filtrirnih elementov prave velikosti.
Maslo vredno filter je zasnovan tako, da daje ravno frekvenčni odziv v pasovnem pasu filtra in se v zaustavitvenem pasu zmanjšuje proti ničli. Osnovni prototip Maslo vredno filter ali je nizkopasovna zasnova ampak s spremembami visoko pasovne in pasovni filtri je mogoče oblikovati.
Kot smo videli zgoraj, dobiček enote visokofrekvenčnega filtra prvega reda je H (jω) = jω / (jω + ω_c)
Za n takih filtrov v seriji H (jω) = (jω / (jω + ω_c)) ^ n ki je ob reševanju enako

‘N’ nadzoruje vrstni red prehoda med pasom prenosa in pasom zaustavitve. Zato višji vrstni red, hiter prehod, tako da pri n = ∞ Filter, vreden masla, postane idealen visokofrekvenčni filter.
Med izvajanjem tega filtra zaradi enostavnosti upoštevamo ωc = 1 in rešujemo prenosno funkcijo
za s = jω, tj. H (s) = s / (s + ωc) = s / (s + 1) za naročilo 1:
H (s) = s ^ 2 / (s ^ 2 + ∆ωs + (ωc ^ 2) za naročilo 2
Zato je prenosna funkcija kaskade v visokofrekvenčnem filtru


Parcela masla Bode vredna visokofrekvenčnega filtra
Uporaba visokofrekvenčnega filtra
Aplikacije visokofrekvenčnega filtra vključujejo predvsem naslednje.
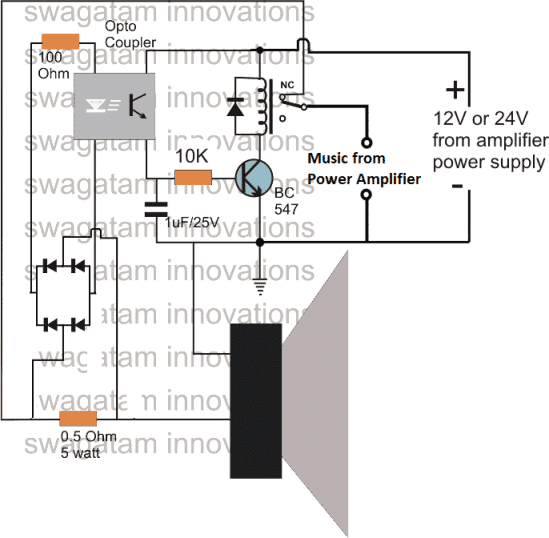
- Ti filtri se uporabljajo v zvočnikih za ojačanje.
- Visokoprepustni filter se uporablja za odstranjevanje neželenih zvokov blizu spodnjega konca zvočnega območja.
- Da bi preprečili ojačanje Enosmerni tok ki bi lahko škodovali ojačevalniku, se za sklopke AC uporabljajo visokofrekvenčni filtri.
- Visokofrekvenčni filter Obdelava slik : Visokofrekvenčni filtri se uporabljajo za obdelavo slik za ostrenje podrobnosti. Z uporabo teh filtrov na sliki lahko pretiravamo vsak majhen del podrobnosti na sliki. Toda pretiravanje lahko poškoduje sliko, saj ti filtri ojačajo šum na sliki.
Pri oblikovanju teh filtrov je treba še veliko izboljšati, da bi dosegli stabilne in idealne rezultate. Te preproste naprave igrajo pomembno vlogo različno nadzorni sistemi , avtomatski sistemi, obdelava slik in zvoka. Katera od vlog Visokoprepustni filter ste že naleteli?