Izračun časa polnjenja / praznjenja kondenzatorja z uporabo RC Constant

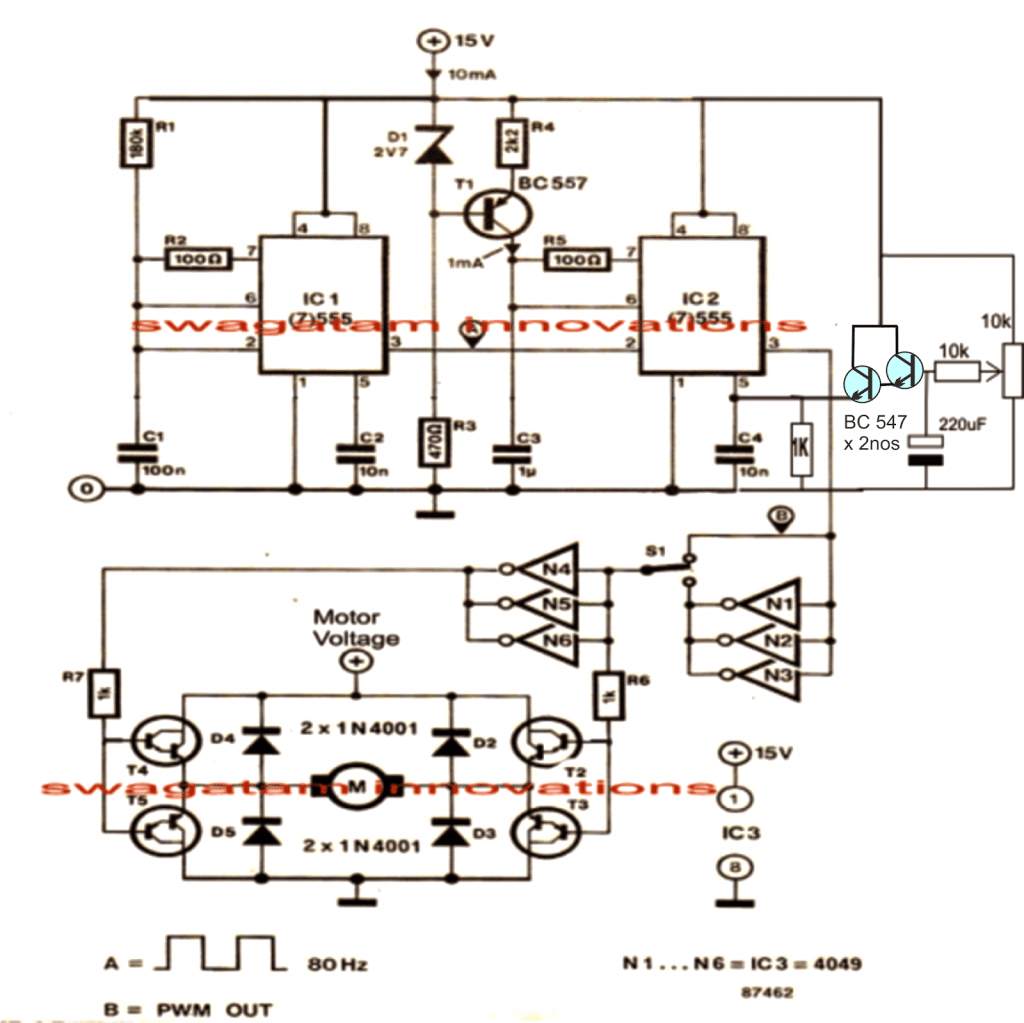
Obdobja polnjenja in praznjenja kondenzatorja se običajno izračunajo z RC konstanto, imenovano tau, izraženo kot zmnožek R in C, kjer je C kapacitivnost, R pa uporni parameter, ki je lahko zaporedno ali vzporedno s kondenzatorjem C. Lahko je izraženo, kot je prikazano spodaj:

τ = RC

RC konstantno tau lahko definiramo kot obdobje, potrebno za polnjenje določenega kondenzatorja skozi pripadajoči serijski upor, z razliko približno 63,2% med njegovo začetno stopnjo polnjenja in končno stopnjo naboja.

Nasprotno pa lahko zgoraj izraženo konstanto RC definiramo kot obdobje, potrebno za praznjenje istega kondenzatorja skozi vzporedni upor, dokler ne ostane 36,8% nivoja naboja.

Razlog za določanje teh omejitev je izredno počasen odziv kondenzatorja, ki presega te meje, kar povzroča postopki polnjenja ali praznjenja da bi skoraj trajalo neskončno veliko časa, da bi dosegel ustrezen nivo polnega napolnjenosti ali polnega praznjenja, zato je v formuli prezrt.

Vrednost tau izhaja iz matematične konstante je , ali

,

natančneje pa se lahko izrazi kot napetost, potrebna za polnjenje kondenzatorja glede na parameter 'čas', kot je navedeno spodaj:

Polnjenje

V (t) = V0 (1 - e ^ −t / τ)

Odvajanje

V (t) = V0 (e ^ −t / τ)

Izrezna frekvenca

Časovna konstanta

τ

je običajno povezan tudi z alternativnim parametrom, mejno frekvenco f c in se lahko izrazi s formulo:

τ = R C = 1/2 π f c

preureditev zgornjega daje :, f c = 1/2 π R C = 1/2 π τ

kjer upor v ohmih in kapacitivnost v faradih daje časovno konstanto v sekundah ali frekvenco v Hz.

Zgornje izraze lahko nadalje razumemo s kratkimi pogojnimi enačbami, na primer:

f c v Hz = 159155 / τ v µsτ v µs = 159155 / f c v Hz

Spodaj so predstavljene druge podobne uporabne enačbe, ki jih je mogoče uporabiti za ocenjevanje tipično RC konstantno vedenje:
čas vzpona (20% do 80%)

t r ≈ 1,4 τ ≈ 0,22 / f c

čas vzpona (10% do 90%)

t r ≈ 2,2 τ ≈ 0,35 / f c

V nekaterih zapletenih tokokrogih, ki lahko spremljajo več kot en upor in / ali kondenzator, pristop s časovno konstanto odprtega tokokroga ponuja način izpeljave mejne frekvence z analizo in izračunom števila številnih povezanih konstant RC.